These are some notes from my final year project. I took some time to get this right in my head at the initial stages, so I thought it will be useful to note it down.
In the project I have been dealing a lot with gravitational lensing by a Schwarzschild black hole. The famous formula for the bending angle (in units of $c = G = 1$) is
$$\alpha = \frac{4M}{R}.$$
This formula forms the basis for one of the key observational confirmations of Einstein’s theory of General Relativity. The Newtonian prediction is only half of the GR result.
In the formula, $M$ is the lensing mass. In the Schwarzschild spacetime, this is the mass of the black hole. But when I first started out on my project, I was a little confused about which distance $R$ was referring to.
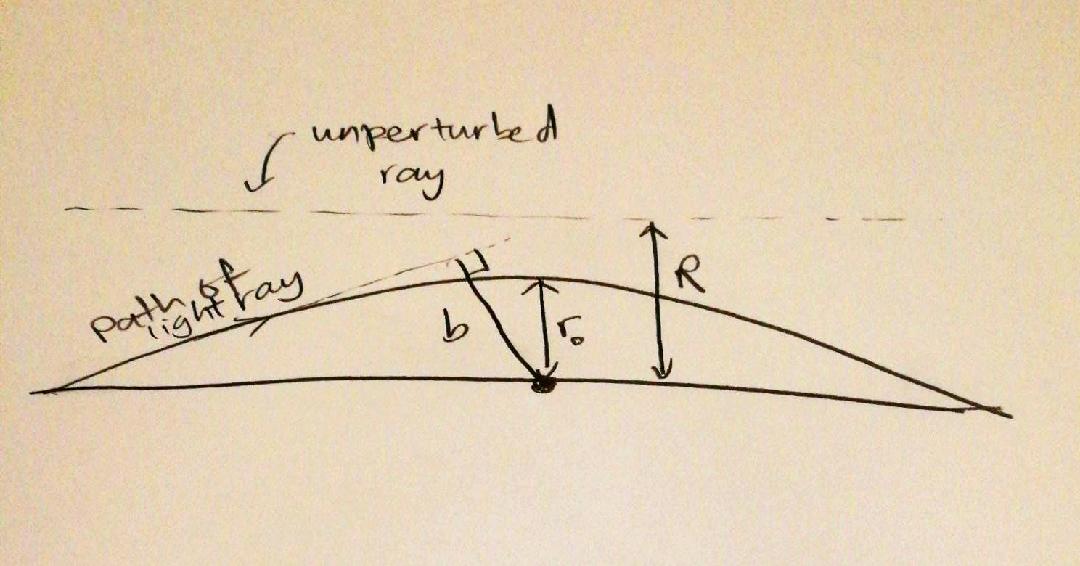
There are 3 distances that are typically used as length measures:
- $b$, the impact parameter, defined as the perpendicular distance between the light path and the black hole
- $r_0$, the distance of closest approach between the light path and the black hole
- $R$, the perpendicular distance between the unperturbed trajectory and the black hole
Their differences between them can be seen in the diagram below.
Most papers use the impact parameter $b$ to parameterize lensing, because it is a physical, measurable quantity (though complications also arise when you throw in a cosmological constant, see Lebedev & Lake, 2013), whereas the distance of closest approach is not so easy to determine, and $R$ is a result of a mathematical construct which (from what I understand), roughly corresponds to the distance at turning point from the black hole assuming the light ray was bent at a single point.
These distances are similar, but not the same. They are all equal to one another to first order. This means that to first order in $M/R$, the bending angle can be written equivalently as
$$\alpha = \frac{4M}{R} = \frac{4M}{r_0} = \frac{4M}{b}.$$
However, they can no longer be used interchangeably from second order onwards. It is easy to convert between them using the relationships between the three distance measures:
$$\frac{r_0}{b} = 1 - \frac{M}{b} - \frac{3}{2}\left (\frac{M}{b} \right )^2 - 4\left (\frac{M}{b}\right )^3 +\ldots$$
$$\frac{R}{r_0} = 1 + \frac{M}{R} + \frac{3}{16} \left (\frac{M}{R} \right )^2 + \ldots$$
For example, here is a table of the second and third order coefficients for the different distance measures:
| 2nd order | 3rd order | |
|---|---|---|
| $M/R$ | $15\pi/4$ | $401/12$ |
| $M/r_0$ | $-4 + 15\pi/4 $ | $122/3 - 15\pi/2$ |
| $M/b$ | $15\pi/4$ | $128/3$ |
If even higher orders are needed, Keeton and Petters (2005) contains a detailed derivation of the lensing formula up to arbitrary order. Most of the time, though, just the first order term will suffice. But in my project I am investigating much smaller effects in gravitational lensing, and the higher order terms are important.